Dependency Graphs in Ruby

Or, Making a Sandwich Using Sidekiq

When something goes wrong with your data, Rewind Backups is there to help you restore it back to the way it was. The process for doing this is actually a little more complicated than one might imagine: every platform Rewind integrates with has its own domain model with its own set of rules. In many cases, a certain piece of data depends on other pieces of data existing beforehand, which puts some limitations on what we can restore and when.

For example, in our QuickBooks Online integration, this means we need to restore Accounts before we can restore the Invoices associated with those Accounts. When performing a BigCommerce restore, we need to make sure a Category exists before we can restore a Product that belongs to that Category.

One time, we tried drawing a diagram of all the item types we restored and what other item types they depended on, thinking we would just “figure out” the order and hardcode something in. There were so many lines in the diagram that we could barely read the words on the screen. It became obvious very quickly that we needed something a little more automated and a little easier to use.

A Bit of Math

Let’s start by dipping our toes into graph theory. I promise it will be over soon.

The situation described above, in which Rewind needs to restore certain pieces of data before attempting to restore others, can be modeled as a graph.

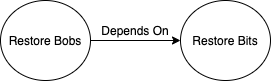
This is called a directed graph, because the edge indicates a specific direction with an arrow. It is made obvious that “Bobs depend on Bits”, and not vice versa. Let’s add more nodes to our example:

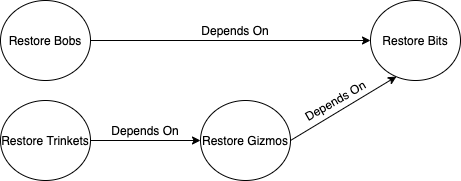
Now it becomes clearer that not only is our graph directed, it is also acyclic: starting from any node and travelling along the edges in any order, you will never come back to your starting node (remember you can only travel in the correct direction). It wouldn’t make much sense in this context if “Bobs depend on Bits” and “Bits depend on Bobs” were both true.

Directed acyclic graphs (DAGs) have an interesting property: they can be topologically sorted. This sorting algorithm has many applications, such as job scheduling or software dependency resolution. The result of applying a topological sort to a DAG is a list of all nodes, specifying a valid order in which they can be resolved. Note that, depending on the graph, there may be multiple valid ways to order the nodes.

If we were to apply the algorithm to our graph above, we might end up with something like [Restore Bits, Restore Gizmos, Restore Bobs, Restore Trinkets]. By following this list, we know that our entire restore operation will be run in the correct order.

Promise kept?

Introducing Dagwood 🥪

Luckily for us, Ruby’s standard library contains a module for doing the heavy lifting involved in a topological sort: tsort. This is a good starting point, but it doesn’t “just work” on its own. We created Dagwood as a kind of wrapper around tsort to hide some implementation details, improve ease of use and add a couple of features that were important for our use cases. Have a look at Dagwood’s ability to return parallelizable node orderings or generate subgraphs, among others.

We’d love for others to get involved. If you have questions, find a bug, or have an idea on how to make Dagwood better, feel free to reach out to us (or open a PR!).

Back to the Problem at Hand

A customer has requested that their data be restored to a point in the past. There are thousands of items needing to be restored, spanning a dozen different types of items, some of which depend on other types being restored first.

We solved the scaling and reliability issues ages ago: we use Sidekiq to process the restore, one tiny job at a time. Sidekiq also has the concept of Batches, which allow you to run jobs in, well, batches. When a batch is complete, a callback is invoked allowing you to schedule the next set of jobs. In theory, you could hardcode the order in which your operations need to run. Imagine something like this, but with way more workers and callbacks:

class RestoreAllBitsWorker
  include Sidekiq::Worker

  def perform
    bits_batch = Sidekiq::Batch.new
    bits_batch.description = 'Restore all Bits'
    bits_batch.on(:complete, RestoreBitsDone)

    # Spawn one worker per Bit to restore
    bits_batch.jobs do
      Bits.each { |bit| RestoreSingleBitWorker.perform_async(bit) }
    end
  end
end

# Once all the Bits are done, this callback will start a worker
# for restoring all the Bobs.
class RestoreBitsDone
  def on_complete(status, options)
    RestoreAllBobsWorker.perform_async
  end
end

This approach presents some challenges for us:

• First, it’s ugly and gets complicated fast. Imagine a workflow with even just 5 or 6 different types of items. It would be a nightmare to follow along, let alone make changes to. Now consider that some of the platforms we interact with have over 30 types of items.
• Second, it’s not platform-agnostic. We would need a separate set of workers and callbacks for every one of the platforms for which we offer restore capabilities. Something a little more reusable would be nice.
• Third, Rewind offers a lot of flexibility to the customer requesting a restore. They may decide to only restore certain item types instead of restoring the entirety of their data. It would be difficult to capture the dynamic nature of these kinds of requests using a static Sidekiq workflow.

Our solution to this problem uses a combination of Sidekiq batches and Dagwood’s ability to generate the correct order of operations for a given dependency graph.

Let’s start by defining all the dependencies between items, and creating a Dagwood::DependencyGraph.

DEPENDENCY_GRAPH = Dagwood::DependencyGraph.new(
  bits: [],
  bobs: %i[bits],
  gizmos: %i[bits],
  trinkets: %i[gizmos]
)

We can then feed that graph into our “initiate” worker, which is responsible for kicking off the restore operation as a whole. This worker is also responsible for creating the batch under which all other work will be done. I won’t define RestoreAllItemsByTypeWorker in this article, but let’s pretend that’s where the magic of actually restoring all the data of a single type (e.g “Trinkets”) happens.

class InitiateRestoreWorker
  include Sidekiq::Worker

  def perform(dependency_graph)
    # This will be an array like [:bits, :bobs, :gizmos, :trinkets]
    order_of_operations = dependency_graph.order

    # This is our top-level batch, containing ALL the jobs for this restore.
    # This batch only completes once every single item has been restored.
    batch = Sidekiq::Batch.new
    batch.description = 'Restore all items'
    batch.on(:complete, RestoreCompleteCallback)

    batch.jobs do
      OrderedWorker.perform_async(
        order_of_operations,
        RestoreAllItemsByTypeWorker
      )
    end
  end
end

The InitiateWorker worker above didn’t actually do much, outside of setting up. The actual work starts when we pass the ordered list of restore types into our next worker:

class OrderedWorker
  include Sidekiq::Worker

  def perform(work_to_perform, worker_class)
    return if work_to_perform.empty?

    current_work, *remaining_work = work_to_perform

    # This work is done within the top-level batch we
    # created in the InitiateWorker
    batch.jobs do
      # Create a child batch for the current work to run in.
      # When it is done, pass along the remaining work to the callback.
      child_batch = Sidekiq::Batch.new
      child_batch.description = "Batch for #{current_work}"
      child_batch.on(
        :complete,
        OrderedCallback,
        'remaining_work' => remaining_work
        'worker_class' => worker_class
      )

      child_batch.jobs do
        worker_class.perform_async(current_work)
      end
    end
  end
end

You may have noticed that the OrderedWorker pops the front of the work_to_perform array and only ends up spawning a single restore worker for a single type. When that type is completely done restoring, we will invoke our OrderedCallback with the remaining types we haven’t restored yet… which will re-invoke the OrderedWorker, until all work has been completed.

class OrderedCallback
  def on_complete(status, options)
    if options['remaining_work'].present?
      Sidekiq::Batch.new(status.parent_bid).jobs do
        options['worker_class'].perform_async(
          options['remaining_work'],
          options['worker_class']
        )
      end
    end
  end
end

All of the above code is simplified, but hopefully the general idea is clear enough: use the dependency graph to organize the work. Perform the first “piece” of work. When it completes, pass the remaining work along to the callback, which will re-enqueue the worker. Repeat until all work is complete, at which point the top-level batch will complete. Done!

At this point we have a functional solution that is reusable and dynamic, but it’s not optimized for speed. The solution above will restore every type of item serially, always waiting on the previous operation to complete before moving on to the next. If you take another look at the graph near the beginning of this article, you may realize that it would be entirely possible to do some of the work in parallel. For example, Restore Gizmos and Restore Bobs both depend on Restore Bits, but they don’t depend on each other, indicating they could be done at the same time. This is why Dagwood provides the ability to return node orders that work in parallel. All we need to do is slightly modify the example above.

# We change our call to `.order` with a call to `.parallel_order`
class InitiateRestoreWorker
  ...
  def perform(dependency_graph)
    # This will be an array like [[:bits], [:bobs, :gizmos], [:trinkets]]
    # Every group in the array represents work that can be done in parallel
    order_of_operations = dependency_graph.parallel_order
    ...
  end
end

# The only change we need to make here is to loop over
# current_work, which is now an Array.
class OrderedWorker
  ...
  child_batch.jobs do
    current_work.each { |work| worker_class.perform_async(work) }
  end
  ...
end

And we’re done! We’ve used Sidekiq to run through a sequence of dynamically generated work, ensuring that we’re doing it in the correct order and in the quickest way possible.

Interested in solving problems like this? Want to get paid at the same time?? Check out Rewind’s open positions to start your career in DevOps, Security, Engineering, and more